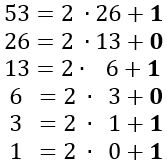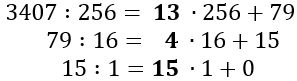Számrendszerek

Számrendszerekről általában

A számábrázolási rendszer vagy számrendszer meghatározza, hogyan ábrázolható egy adott szám.
A számjegy egy szimbólum (vagy azok csoportja), ami egy számot ír le.

A számjegyek éppen úgy különböznek az általuk leírt számtól, mint egy szó attól a dologtól, amit valójában jelent.
A "11" jelek a "tizenegy" és a "XI" különbözőek, de ugyanazt a számot írják le.

Egy számrendszer (vagy számábrázolási rendszer) egységes szabályok alapján meghatározza, hogy számjegyek sorozata milyen számokat jelenít meg. A használt ábrázolási rendszer meghatározza, hogy a "11" számot a bináris háromnak, vagy a decimális tizenegynek, vagy a hexadecimális tizenhétnek, vagy a használt számrendszer alapszámának függvényében más számnak kell érteni.

10-es számrendszer

Az ismert 10-es számrendszer helyiérték táblázata:

10-es számrendszer

A beírható számok alaki értéke 1-gyel kisebb, mint a számrendszer alapszáma. Itt 10-es számrendszernél a helyiértékekre beírható számok alaki értéke 0…9.
Attól függően, hogy az adott számjegy milyen helyi értéken szerepel, más-más értéket vesz fel.
Például a 35,405 számnál első 5-ös alaki értékű szám az 1-es helyiértéken szerepel így valódi értéke (helyértéke) 1. A második 5-ös alaki értékű szám az 1 ezred helyiértéken szerepel, így valódi értéke (helyértéke) 5 ezred.
A második 5600,0012 számban az 5 alaki értékű szám az 1000 helyiértéken szerepel, így valódi értéke 5 000.

Q alapú számrendszer

A számrendszerbe beírható számjegyek alaki értéke a 0 ... (Q-1) termsézetes számtartományba esthet.

A táblázat alapján a fent megadott számtartományba eső alapszámot választhatunk.

Kettes (bináris) számrendszer

A számrendszer alapszáma: Q=2.
A számrendszerbe beírható számjegyek alaki értéke a fentiek alapján 0; 1 természetes számtartományba esthet.

Az adott számrendszer helyirték táblázata:

A kapott számot a következő módon kell kiolvasni: 6 egész 75 század tizes számrendszerbeli szám kettes számrendszerbeli alakja egy - egy - nulla kettedesvessző egy - egy.

Szám átváltása 10-es számrendszerből 2-es számrendszerbeli számmá:

Váltsuk át az 53 tizes számrendszerben adott számot kettes számrendszerbe.

1. módszer: Megnézzük, hogy a helyiérték táblázat szerint melyik az első olyan helyiérték, mely kisebb, mint az adott szám.
Ezzel a helyiértékkel osztjuk el a számot, s kiszámítjuk a maradékot. Itt az 53-nál kisebb első helyiérték a 32. Azt követően a maradékot osztjuk a következő helyiértékkel (16), majd az azt követővel (8), stb. mindaddig, amíg a maradék nulla lesz.

A kapott hányadosok értékei (itt félkövéren kiemelve) ebben a sorrendben írva adja a szám 2-es számrendszerbeli alakját.

Kiolvasva: ötvenhárom a tizes számrendszerben egyenlő egy - egy - nulla - egy - nulla - egy a kettes számrendszerben.

2. módszer: Az Euklideszi algoritmust alkalmazzuk. A decimális számrendszerbeli számokat tizenhattal való maradékos osztással tudjuk hexadecimális számrendszerbeli számmá alakítani.Az átalakítandó számot oszd el tizenhattal. Minden osztásnál jegyezd fel a maradékot.Addig folytasd az egészrésszel való osztást, amíg nulla hányadost nem kapsz.

A kapott maradékokat alulról felfelé leírva kapjuk az adott szám bináris alakját.

Nyolcas (oktális) számrendszer

A számrendszer alapszáma: Q=8.
A számrendszerbe beírható számjegyek alaki értéke a fentiek alapján 0..7 természetes számtartományba esthet.

A 8-as számrendszerben megadott számokat a következő módon kell kiolvasni:

Az első szám: hat - kettő - nulla a nyolcas számrendszerben 400-at ér a tizes számrendszerben.
A második szám: öt - hét nyolcados vessző három értéke a tizes számrendszerben 47 egész 375 ezred

16-os (hexadecimális) számrendszer

A számrendszer alapszáma: Q=16..
A számrendszerbe beírható számjegyek alaki értéke a fentiek alapján 0..15 természetes számtartományba esthet.
Egy helyiértékre viszont csak egy számjegy írható, így nem lenne használható a 10..15 szám. Helyettük az ABC megadot karaktereit használjuk: 10=A ; 11=B; 12=C; 13=D; 14=E; 15=F.

Szám átváltása 10-es számrendszerből 16-os számrendszerbeli számmá:

Váltsuk át a 3 407 tizes számrendszerben adott számot 16-os számrendszerbe:

1. módszer: Megnézzük, hogy a helyiérték táblázat szerint melyik az első olyan helyiérték, mely kisebb, mint az adott szám.
Ezzel a helyiértékkel osztjuk el a számot, s kiszámítjuk a maradékot. Itt a 3407-nél kisebb első helyiérték a 256. Azt követően a maradékot osztjuk a következő helyiértékkel (16), majd az azt követővel (1). Így a maradék nulla lesz.

A kapott hányadosok értékei (itt félkövéren kiemelve) ebben a sorrendben adja a szám 16-os számrendszerbeli alakját, figyelve arra hogy a 10-től kezdve nagy betűket írunk a fent leírtak szerint. Itt a 13 helyett D, a 15 helyett pedig F-et írunk.

2. módszer: Az Euklideszi algoritmust alkalmazzuk. A decimális számrendszerbeli számokat tizenhattal való maradékos osztással tudjuk hexadecimális számrendszerbeli számmá alakítani.Az átalakítandó számot oszd el tizenhattal. Minden osztásnál jegyezd fel a maradékot.Addig folytasd az egészrésszel való osztást, amíg nulla hányadost nem kapsz.

A kapott maradékokat alulról felfelé leírva kapjuk az adott szám hexadecimális alakját , figyelve arra hogy a 10-től kezdve nagy betűket írunk a fent leírtak szerint. Itt a 13 helyett D, a 15 helyett pedig F-et írunk.

60-as számrendszer

A 60-as számrendszer nyomait fedezhetjük fel a szögek és az idő mérésénél..
A szög fokban történő mérésénél 60 a váltószám. (1°=60 szögperc, 1 szögperc 60 szögmásodperc).
Hasonlóan az időnél (1 óra=60 perc, 1 perc= 60 másodperc).

Tárgymutató kulcsszavai

Számrendszerek